数学感悟

无标签

Math

发布之期: 2021-12-10

更新之期: 2022-05-10

文章字数: 7.1k

阅读时长: 25 分

阅读次数:

数学是一门计算的学问，不断组合现有结论达到 ”巧妙计算“，但当技巧穷尽，还有一门研究如何暴力计算的数值分析，这需要借助计算机，而机器学习依靠的就是这些。

许多内容是个人直觉感悟，可能有错

纯粹数学：不顾与现实的几何，单单研究数学本身，以数论为主体。

计算数学研究的是如何在找不到公式解的情况下（比如超越方程）找到近似解，而数值分析就是研究如何用计算机来完成这一过程，是计算数学的主体部分。

包括矩阵计算【数值线性代数】

线代是研究【线性】的学科，因为人类在线性领域研究颇深。而矩阵是线代的一种表示工具。

矩阵经过发展，形成了独立的数学分支——矩阵论。

具体数学是教你如何把一个实际问题一步步演化为数学模型，然后通过计算机解决它，特别着重于算法分析方面。算法偏向于将理论转变为高效的程序。【我才懒得搞这个。。卷死了】

微积分：解决了无穷小的定义问题，严谨的用极限来分析计算问题。

数学分析是分析学的基础，包括了微积分，又拓展了级数、复数和更多的函数域。

泛函分析：研究对象是函数构成的空间，看作无限维向量空间的解析几何和数学分析。

拓扑是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的一个学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。

统计学是通过搜索、整理、分析、描述数据等手段，以达到推断所测对象的本质，甚至预测对象未来的一门综合性科学。分为描述统计和推断统计，代表了完成统计的两个过程。这也是类似心理学的，结合了大量的领域知识。有几分估算，有些玄幻。。。变魔术。

数理统计以概率论为基础，研究大量随机现象变化规律的一种方法。精准

问题

reflection = 2projection - I
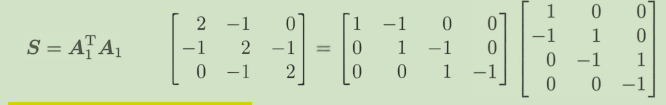分解怎么分的
连续求偏导，af/ax * af/ay

理论可以分学派，但是这只是由基本假设不同而探索的不同路径，对于理论家们，只是选择了一个方向继续研究而已，而不是什么党派斗争。

微积分

所谓极限，强调的是存在性，只要极限存在，那么不论你需要多高的收敛精度，总能做到。
导数只能研究一维，微分可以研究更高维度的
泰勒是对函数更高层导数的拟合。
反常和级数收敛是找到“无限中的有限”
对二元函数来讲，z=f(x,y)三维空间中的一个曲面，在某点可微意味着在该点有唯一切平面，也就是说平面上通过该点的所有曲线有切线，且所有切线共面。

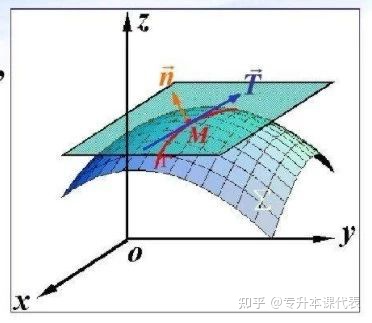
因此有可微->偏导存在 + 函数连续

而可微的充分条件：每个正交方向上的偏导数都在小邻域内存在连续，则是因为正交基线性组合可以铺满整个空间（二元方程就是二维空间），确保能完成超平面的效果。
输入参数（几元）每多一个，反向传播就提高几倍效率，因为节省了重复计算。
导数除了理解为”趋势“，还可以理解为”权重“，在F（x,y,z）的求隐函数例子中，x，y，z相互之间的导数与对整体F偏导有关，这里就反映了权重的关系，谁的权重大，对整体的影响就大。

比如：

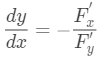
假如，Fx/Fy比较大，证明x影响大，所以dy/dx大，代表x能替换更多的dy。负号是因为那一点是固定的，每多一点x，就要减少那么多y才能维持不变。
【人们好像默认选用正交的参数或基底】，而方向导数就是线性组合正交基来表示任意方向。
我是这样理解高阶泰勒的，这其实就是多了个链式法则，从低纬度一步一步组合到最高的维度，根据链式法则来穷尽所有的组合，因为每一步都要考虑不同正交基间的相互影响。而这种线性组合的穷尽，当然用线性代数里面的矩阵比较好表示一些，也就是黑塞矩阵

结论

曲线求的是切线和法平面，用的是导数，

曲面求的是切平面和法线，用的是偏导数。

概率论

分布列对于随机变量的每个取值给出对应的概率。它对应的是X的值也就是值域而不是x的定义域

卧槽，我发现诡异的地方了。。。x在这里是X的取值，而不是基本事件的定义域。。。tmd

在概率论里面，“随机变量”好像才是第一层。。。而它本身就是一个映射规则很奇怪的函数、、
各种定律乱七八糟的，其实还不就那几个思想：

分组（全概率），序贯（乘法定理），条件就是选取更小的样本空间然后继续分组，贝叶斯就是部分/整体。独立性要区分。。玄学。

独立性和条件独立性并没联系。

两两独立和相互独立也没关系。这个独立非常玄学。它根本没用普通的数学关系表示出来，因为数学不能刻画现实的所有逻辑，哪怕是离散数学，也只能刻画部分而已。

全期望 P92，【无条件平均（期望）可由条件平均（条件下的期望）再求平均得到】
连续和离散贝叶斯 P160
重期望法则 P195 条件期望的期望 = 无条件期望（全期望的另一版本）
全方差法则 P199 总方差可分为组内方差平均数 + 各组间的方差（有物竞那味了）【这俩可用来化简】
理论依据：估计$E[X|Y]$ 与估计误差$E[X|Y]-X$ 相互独立
矩母函数（变换）是对概率（分布律/概率密度函数）的另一种表述，不太直观，单解决某些类型的数学计算很方便
$M_X(s) = E(e^{sX})$ 矩母函数是参数为s的函数。即矩母函数作用于一个函数得到一个新的函数。
$M_Y(s) = E(e^{s(aX+b)}) =e^{sb}E(e^{saX}) = e^{sb}M_X(sa)$ 标准正态分布$M_Y(s) = e^{s^2/2}$ 一般$M_X(s) = e^{(\sigma^2s^2/2)+\mu s}$
$M_X(0) = 1$ $\displaystyle \lim_{s\rightarrow -\infin}M_X(s) = P(X=0)$
独立随机变量和与矩母和的矩母为随机变量矩母之积 P207 常见分布矩母函数表 P208-209
随机数个相互独立随机变量之和的均值、方差、矩母

随机过程
是处理包含时间以及数据序列的概率模型。
序列中的每个数据都视为一个随机变量，简单地说，随机过程就是遗传（有限或无限）随机变量序列。
特征：强调过程中产生的数据序列之间的相关关系、对整个过程的长期均值感兴趣、刻画边界事件的似然或概率
种类繁多，本书仅讨论：到达过程、马尔可夫过程

到达过程：“到达”特性是否发生，研究相邻到达时间是相互独立的随机变量的模型，根据服从几何、指数分为伯努利、泊松过程。
马尔可夫过程：未来数据演化与历史数据有概率相关结构，但假设未来数据只依赖当前数据，与过去数据无关，技术十分成熟。

与伯努利相比，泊松是连续时间轴上的到达过程。其性质见269

	泊松	伯努利
到达时间	连续	离散
到达次数分布(可加)	泊松(参数为$\lambda \tau$)	二项
相邻到达时间分布(独立、无记忆)	指数	几何
到达率	$\lambda/$单位时间	$p/$每次试验
第k次到达的时间	埃尔朗\伽玛分布 P272	帕斯卡分布 P261

到达次数随机变量是相邻到达时间随机变量之和：$Y_k = T_1+…+T_k$

P262 伯努利过程的分裂与合并，仍是伯努利，$pq\ p(1-q)\ (p+q-pq)$

P274 泊松过程分裂合并类似，$\lambda p$ $\lambda_1+\lambda_2$

P277 随机数个独立随机变量和的性质。

随机插入悖论，由于插入时，插入不同区间的概率不同，进行修正。泊松过程将区间修正为二阶埃尔朗分布，其他过程也会有影响。

马尔可夫模型中，未来会依赖过去，影响归结为对状态的影响，变量取值有限。
马尔可夫模型哪里都有，包含了几乎所有的动力模型，状态随时间变化具有不确定性。同分离散、连续

线代和矩阵论

线性代数最让人陶醉的是，它非常自然的引出了多维空间的概念，即使我们想象不出来。由于科学研究中的非线性模型通常可以被近似为线性模型，使得线性代数被广泛地应用于自然科学和社会科学中。非线性的问题极为困难，我们并没有足够多的通用的性质和定理用于求解具体问题。如果能够把非线性的问题化为线性的，这是我们一定要走的方向！

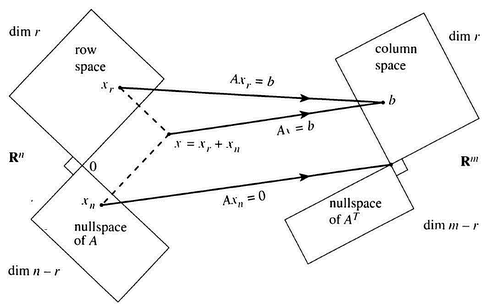
v2-736ecb905966099feac5e943e365aa6f_r

还有什么能比这更牛逼的图？

Ax = b A作用于x，x默认是一列，对A的各列进行线性组合得到向量b

也可以理解为，n维的向量，经过空间变化（A），得到m维对应的结果b

这是线代的基石（为什么不用行？因为约定向量是按列的，所以这样更有意义）
矩阵乘法也很好解释，投影到的空间作为下一个变换的输入空间必须同维度
为什么行变换不改变结果？

我觉得是因为一个向量的各个正交维度是等价的，不管怎么调换顺序，正交带来的对称性是不会被打破的。

而不同特征间组合相当于构建新特征？仍不能由原有的单个特征表出，保留了无关，而在现实问题中，如果要这样操作，就要用学长说的标准化，化为同一量纲。
四种方法：
- 硬算，左行*右列，一个一个傻傻的算
- 左行*右边整个 / 右列*左边整个（我喜欢这个）
- 左列*右行，用很多相同大小的秩一矩阵求和。
线性代数主要以运算为主，比如矩阵的四则运算、行列式的计算、特征值和特征向量的计算等。而矩阵论主要以变换为主，它利用线性代数知识，描述线性变换，并提出了特殊变换，如正规变换、酉变换等。
A B 可逆，A+B不一定可逆，但是AB可逆，我感觉，如果可逆，代表该变换是同维度变换，充斥整个空间的所有可能，AB相当于连续进行两次这样的变换，因此仍是可逆的。
LU分解，一开始分出的是L逆 + U，把L逆取逆后得到的L中（逆的基本矩阵E操作顺序是反的）是从下层开始操作的，因为不会有从上层操作而带来的”干扰项“。
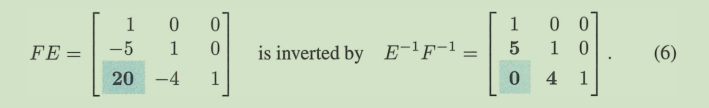
梳理一下，求Ax = b有高斯消元和LU分解；

求Ax = 0，通过给自由变量挨个设1，找到特解。通过设自由变量均为0找到特解。。
With rank one, Ax = 0 is easy to understand. That equation u( v T x) = 0 leads us to v T x = 0. All vectors x in the nullspace must be orthogonal to v in the row space.
U tells which columns are combinations of earlier columns (pivots are missing). Then R tells us what those combinations are.
今天终于能总结理解了。

r = m < n的时候，肥矮，零空间有除了零向量以外的向量，且列空间 = 整个空间，一定有解且有无穷解。

r = n < m的时候，瘦高，列向量张成的子空间处于更大的空间中，因此b可能落不到子空间里，可能无解，零空间也没别的，最多一个解。

r < n,r < m 的时候，零空间一定有别的，列空间小于整个空间，所以要么无解，要么无穷解。

r = m = n 的时候天选之子，只有唯一解。相当于是在研究的整个空间内进行自己到自己的的变换，输入，输出都在整个空间，因此也具有传递性。

能投影出b的x必定有唯一的一部分来自行空间，配上零空间的任意部分，第五版的图画得好啊

顺便提一个结论，空间变换降维的过程是不可逆的，可逆一定是同维。

列秩 = 行秩，用到的结论是基变换（至少在这里）不改变无关的性质。等后面学了基再看吧。
矩阵加减，各个维度相加减，既有新开拓的，又有归零降维的。因此秩应该处于|r1|+|r2|

到 | |r1| - |r2| |之间吧
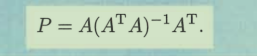
A T A (nxn) is invertible if and only if A has linearly independent columns.

A 是 rectangular ，一定不可逆，不然哪里需要求近似解，

这不是正规方程吗！A表示输入，后面仨 + y就是正规方程，乘起来就是投影，这就是”最小二乘“的几何学表示，代数学表示就是梯度下降令导数均为0.

When Ax= b has no solution, multiply by A T and solve (A T A)x= (A T) b

Ax = b = p+e 其中p落在列空间，e落在左零空间，当无解时，移除e，Ax` = p必然可解。

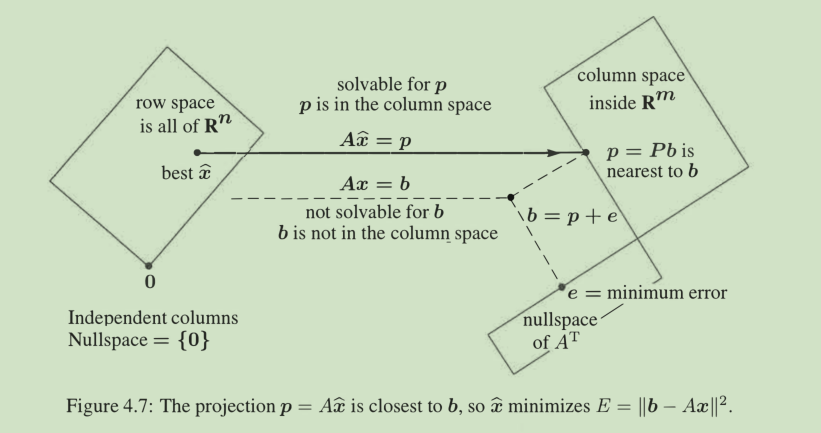
当列不独立时，零空间有除了零向量以外的向量，这时候投影条件无助于找到最小二乘法的直线，要用到伪逆，这时候x` 有多个解，伪逆会选出x最小的解。。。

最小二乘还可适用于非线性方程和傅里叶级数等。
正交矩阵变换并不会影响长度（IIQx ll = ll x ll for every vector x.）,最标准的基，带来最标准的影响。因此对计算非常有利，计算机尽可能采用正交矩阵。

此时最小二乘：

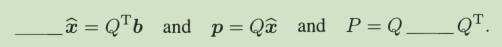
p = Q QT b，若更进一步，Q是方阵，那b = p，直接消干净了。
克拉默法则，给出了我们一个用行列式写出nxn线性方程组解的简便方法，有重要的理论意义，但是计算量很大，所以就是用来理论研究推导的嘛。。
特征值和特征向量引出了新的领域，当我们不再观察单个状态，引入连续的变化后，我们更关注保持不变的东西——特征，这大大简化了各方面的复杂度（比如A^10000）。
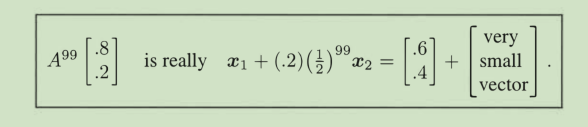
Markov matrix：Each column of P adds to 1 (property)

Its largest eigenvalue is λ = 1，so others are generally disappearing
当进行行变换时，特征值一般会改变，因为特征值虽然刻画的是不变量，但可能是几个不好的基糅杂在一起，而不是像单个基一样分开来，所以好像有个感觉上的“牵连作用”？(待定)
相似性，说明的是不同基下的同一个变换/图形，而对角矩阵其实是因为变换到了特征向量为基的坐标系下，除去了干扰，彻底把特征值暴露出来。

Cx = λx. Then BCB- 1 has the same eigenvalue λ with the new eigenvector Bx

因为这转换到了B基的空间，自然也要把原来的特征向量左乘B转过来。
当代数重数 > 几何重数时，可能是巧合导致某几个方向上λ值相等。

也有可能是因为这几个方向重叠了，对应（A-λI矩阵不可逆，所以转换后降维了）而重叠的情况下我们就少了几个特征向量（被压缩），这就是解释。
uk = A^k *u0 求这种问题

思路是把U0表示为特征向量的线性组合，然后分开研究不同向量k次迭代后的值，再组合起来，过程中组合系数不变。

系数为 c = X-1 u0 这样就组合成了u0（当然比较少的时候也能直接看出来）

然后左乘对角阵的k次方，这是应用k次迭代的特征值到每一个c上得到新的系数，

最后再组合起来

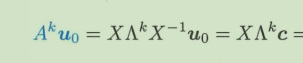
就完成了。
也可以运用在将常系数微分方程转化为线性组合。

只适用于常微分方程就是 dy/du = Cu这种，
对称矩阵时最重要的矩阵，在线代理论和应用上。

它具有n个实特征值，而且有n个正交的特征向量，也必然能被对角化，而且对角化的形式是特征向量矩阵归一化夹着特征值矩阵。

对称矩阵的列空间和行空间是一样的，因此零空间也同时垂直列空间。

【证明用的是数学里的谱定理和几何、物理里的主轴定理（特征向量指向椭圆的主轴）】

而且那个X矩阵这个时候是一个正交矩阵Q，不过注意要选择合适的长度，使得每个向量length = 1
正定矩阵的性质让它更加特殊！但是这并不意味着稀少，它是许多应用的核心。

有一个结论👇因为：显然xT(S+T)x分解后的和恒>0，而对称矩阵相加仍然对称。

If S and T are symmetric positive definite, so is S + T.

可逆和可对角化并没有必然联系。

ATA一定是对称、半正定、可对角化的，如果A还是列满秩，那么ATA一定是可逆、正定的。

对称矩阵可逆的充要条件是n个实特征值不包含0.

strang给出了三种分解方式，我没看懂A1是怎么做到的。
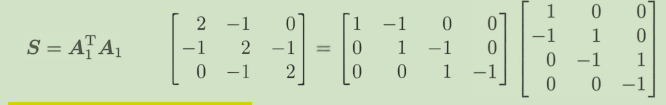
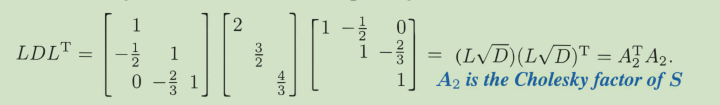
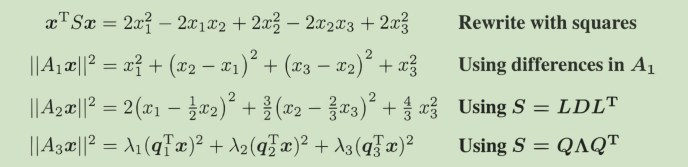
主轴定理：

特征向量指向椭圆的主轴，而且大的特征值对应了短轴。因为半轴是取1/根号下λ

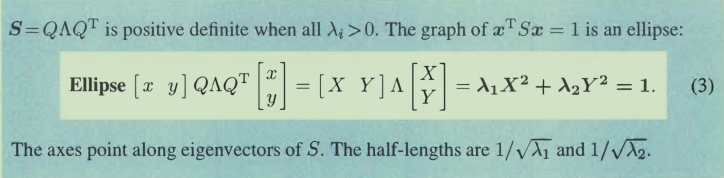
如果有个特征值是负的，那椭圆就变成双曲线了。。。hyperbola，两个特征值均负无实数解。

如果S是nxn的，那么这个就是超椭圆。
正交矩阵矩阵转置 = 矩阵的逆，先从行空间投向列空间，再投回来。 ATA= I啥都不变

那么普通矩阵可逆呢。必然可逆，因为是从原空间投向原空间，但为啥不等于 I 呢，是因为第一次只投到列空间，没有左零空间的部分（而且零空间的被吞掉了），所以往回投的时候定义域缩窄了。那么正交矩阵是没有零空间和左零空间的，完全可逆。
SVD

图像压缩有两种方案，提前选基【傅里叶等】和适应性选基【SVD等】

图像一般是满秩的，但是有很多特征值非常小的可舍弃，

但是有几个问题，一般图像的特征向量不是正交；而且要分解成U,V俩矩阵，这就是SVD能做的。

U和V一定是酉矩阵【即正交矩阵】，因为特征值被抽取出来到 Σ 里了，简易证明

（当A是正定或半正定时特征值分解就相当于是对角化。）

也就是行空间的v投影到列空间的u上，而且系数是σ。

而且σ1 - σr都是正的，因为Ar 满足列满秩，所以ArTAr一定正定，所以特征值都正，开方也正。而紧接着说明了剩下的u和r因为空间的性质，自动正交于列空间和行空间的u 、v，因此Av = uσ 适用于所有的。也说明了对于形状任意，秩情况任意的矩阵，奇异值分解都成立。

相对于对细小变化做出反应的特征值，奇异值对此并不敏感，因为其本质——分解成秩一矩阵。并不会关注细小的变化，而新增的小秩一矩阵自然会分配小奇异值，影响并不大。

类比S = ATA 的对角化

A和S的秩相等，λ = σ2 vi = S的特征值qi。

然后递归的进行这个过程，可以证明这两条式子其实是一样的。

证明用到了瑞利xxx，可见P376页。

那么λ和σ事实上是如何计算的呢？直接暴算多项式（n = 10000+）就太离谱了。。
- 首先要尽可能多搞点0出来，还不能改变任意的σ和λ，这通过巧妙的对角化方法实现。
  
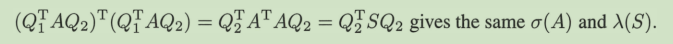
  这样既不改变值，又能用不对称的Q1和Q2操纵矩阵。细节在11节。
- LAPACK提供的受欢迎的方式使用简单的正交矩阵Q来拟合 QT S Q = 特征值对角阵，近似解。
主成分分析

S = AAT/(n-1) 样本协方差矩阵，其中对角线是方差，其他是协方差，A要进行均值化处理

令 T （trace）= σ1^2 +σ2^2 …………，则σ1^2 / T 就代表了重要比例。当比例足够时就可以舍弃后面的。

在这里也同时解决了正交距离最小化，而不是一般最小二乘法的垂直距离。

我们将aj分解到组成他的u1，u2上，

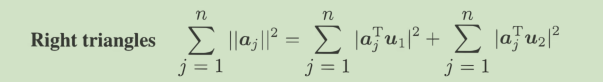
左边的是固定的，当我们在PCA中选择u1作为基，左边第一项最大，则第二项最小，而第二项正是所谓的正交距离，也就是aj落在正交于最优直线的垂线的分量。

当然在处理现实数据时，如果规模是个问题，还要用相关矩阵。统计和线代关系密切。
伪逆真是方便A+ = VΣ+UT

这俩👆是因为投影的时候清除了了垂直的分量。
Are all linear transformations from V = R n to W = R m produced by matrices?

The answer is yes! This is an approach to linear algebra that doesn’t start with
matrices. We still end up with matrices-after we choose an input basis and output basis.

Transformations have a language of their own. For a matrix, the column space contains all outputs Av. The nullspace contains all inputs for which Av = 0

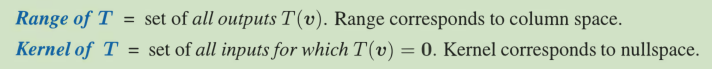
我们只要知道了一组基的变换情况，我们就知晓了变换的一切。
达到一种变换T有很多矩阵，我们希望能找到最好的那种（对角）

线性变换中，把输入向量用vj组合，然后对每个组合进行T变换，再组合起来就是核心idea。

当基变换时，T（v） = v的矩阵就不再是 I 了，而是👇，这样相当于用新基W表示完全相同的向量

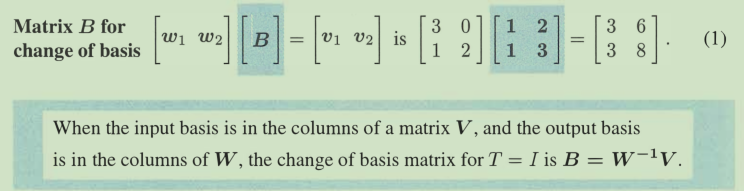
虽然每家教材的形式都不一样，但其实说的都是同一件事啊。感觉这种把V用W表示出来才更直观！

新基下的坐标 = B *原基下的坐标。

变换矩阵A构造如下：

对每个vi，我们用T（vi）将它进行变换，然后用output空间的新基表示出来，

然后这些系数就成为空间变换矩阵A的第一列。

当我们选择特征向量作为我们的基时，这个所谓的A就是特征值矩阵。

结论

Diagonally dominant matrices are invertible

即aii > Σaij (i ≠ j)
LU分解中，A行首的0由L继承，列首的0由U继承，可以省下计算步骤

这样既可以省下计算步骤，又可以直观记录我们高斯消元的过程。关键是这是预处理。

Solve Le = b and then solve Ux = e

对称矩阵的L和U是对称的（LDU），所以不用存两遍。

一般用PA = LU（提前置换好）而不是 A = L1P1U1
函数空间F是无限维度的，他的子集P或Pn是幂函数空间
正交矩阵（包括旋转、置换、反射矩阵），逆 = 转置，

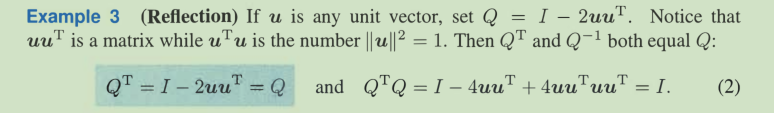
把u方向的向量转成 -u
QR分解法是三种将矩阵分解的方式之一。这种方式，把矩阵分解成一个正交矩阵与一个上三角矩阵的积。QR分解经常用来解线性最小二乘法问题。QR分解也是特定特征值算法即QR算法的基础。

A T A = (QR)T QR = R T Q T QR = R T R

The least squares equation A T Ax =A T b simplifies to R T Rx = R T Q T b.
Then finally we reach Rx = Q T b: good. x = R-1 QT b

这样就不用求解Ax = b，直接回代 👆，非常快，最大的消耗在mn2的乘法（分解QR）。
The determinant is a linear function of each row separately (all other rows stay fixed).
Markov matrix: Each column of P adds to 1, so , 1 is an eigenvalue.

Pis singular, so, 0 is an eigenvalue.(其实0特征值对应的特征向量fills in nullspace)

【别和特征向量fill in A-λI 的零向量空间弄混，而且因为x一定有非零解，所以绝对det = 0】

P is symmetric, so its eigenvectors ( 1, 1) and ( 1, -1) are perpendicular.
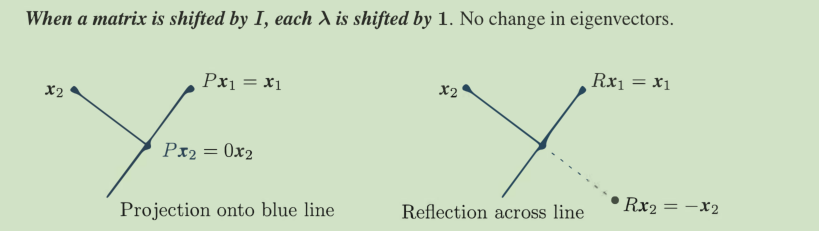
对于相同的特征向量，有 reflection= 2(projection) - I
当2x2矩阵有一个0特征值的时候，每个A-λI的每行都来自一个行向量(a,b)，而对应的特征向量就是(b,-a)
A and B share the same n independent eigenvectors if and only if AB = BA.
实数特征值让特征向量伸缩，而虚数让其旋转

对称矩阵只有实数特征值，反称矩阵只有虚数特征值。
注意，可逆性和可对角化没有关系。可对角化需要的是独立的n个特征向量，可逆性关注特征值为不为0。
线性变换可以用基 * A来表示。

过渡矩阵一定可逆，一个线性变换在不同的基下是相似的，这也暗含了其实是同一个空间的两组基。

我们也可以用奇异值分解来完成这个

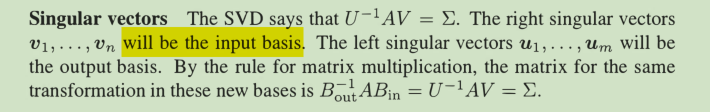
这时称作：isometric 等距，而不是相似。

这里的B就是原基到bi基的过度矩阵。👇
Jordan会构造广义特征向量，而这些特征向量依附于共享特征值的真特征向量：

这是为了尽可能地接近对角化！

同时还有个结论，当矩阵拥有相同的Jordan型时他们相似，没有例外。
好基：离散值是向量，连续值是函数。它们可能不能对角化A，但是对应用数学里的很多重要矩阵，它们能达到接近的效果，更重要的是它们直接选定，无需计算。

傅里叶基，λ^n = 1 ，作用是对角化了n阶置换矩阵。Px = λx，P^2x = λ^2 x。而且适用于P。。P^n 的线性组合的所有矩阵。但是

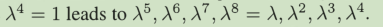
其中，傅里叶基因其周期性而特别适用于周期性的

其中6是将幂级数进行正交化的结果，7是将x对应三角函数以便使用快速傅里叶变换。